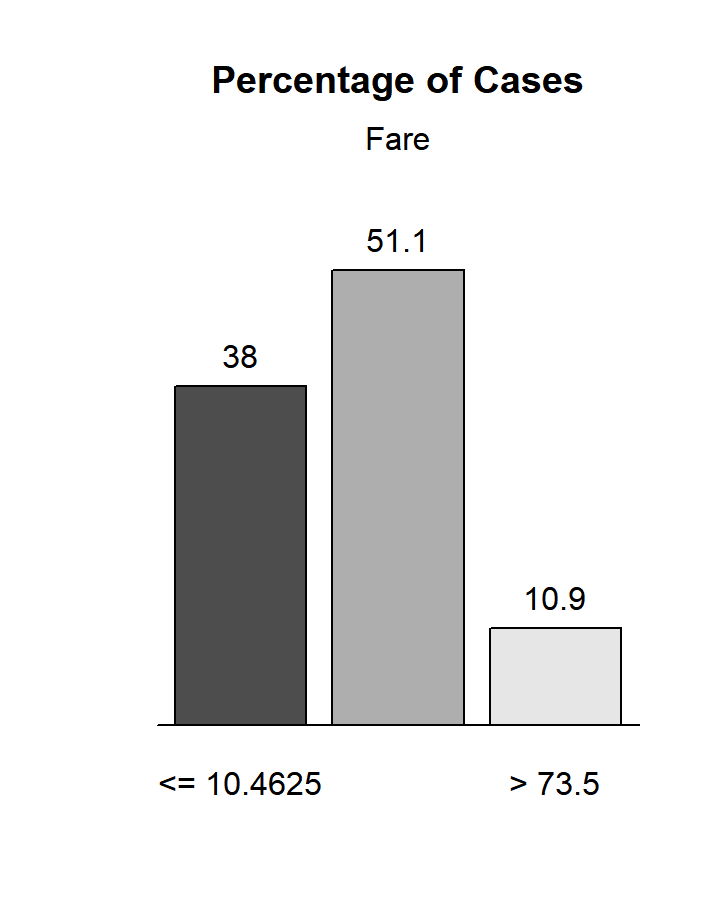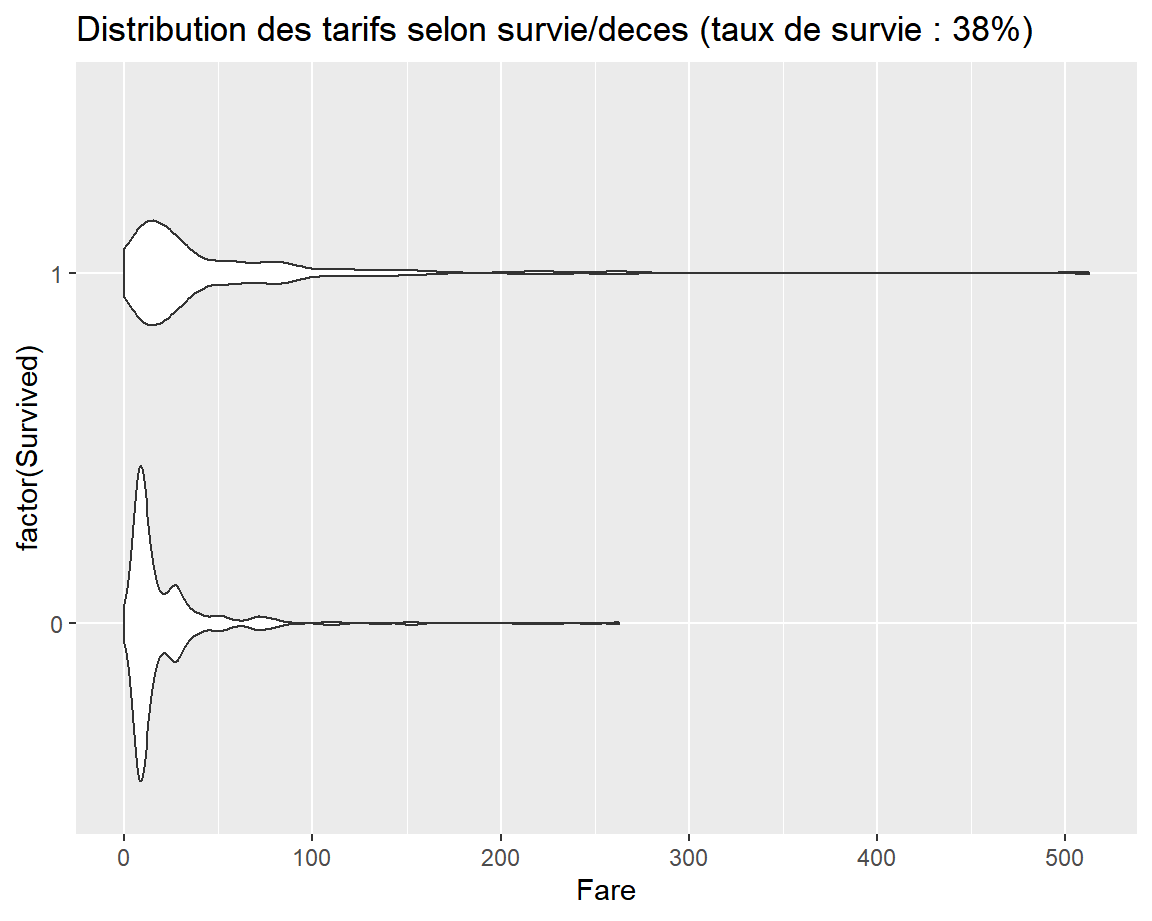
Lien entre la variable Fare et la cible Survived

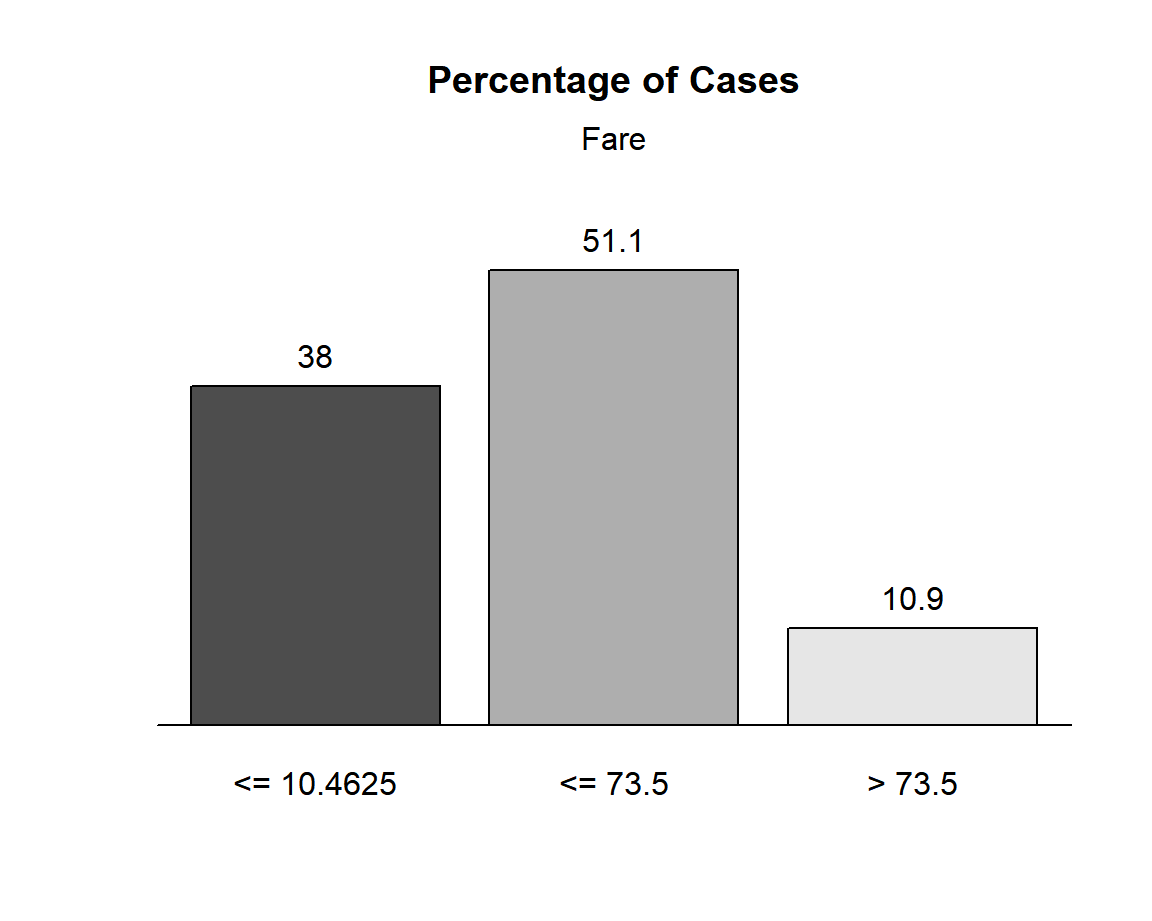
Frequence de chaque modalite creee

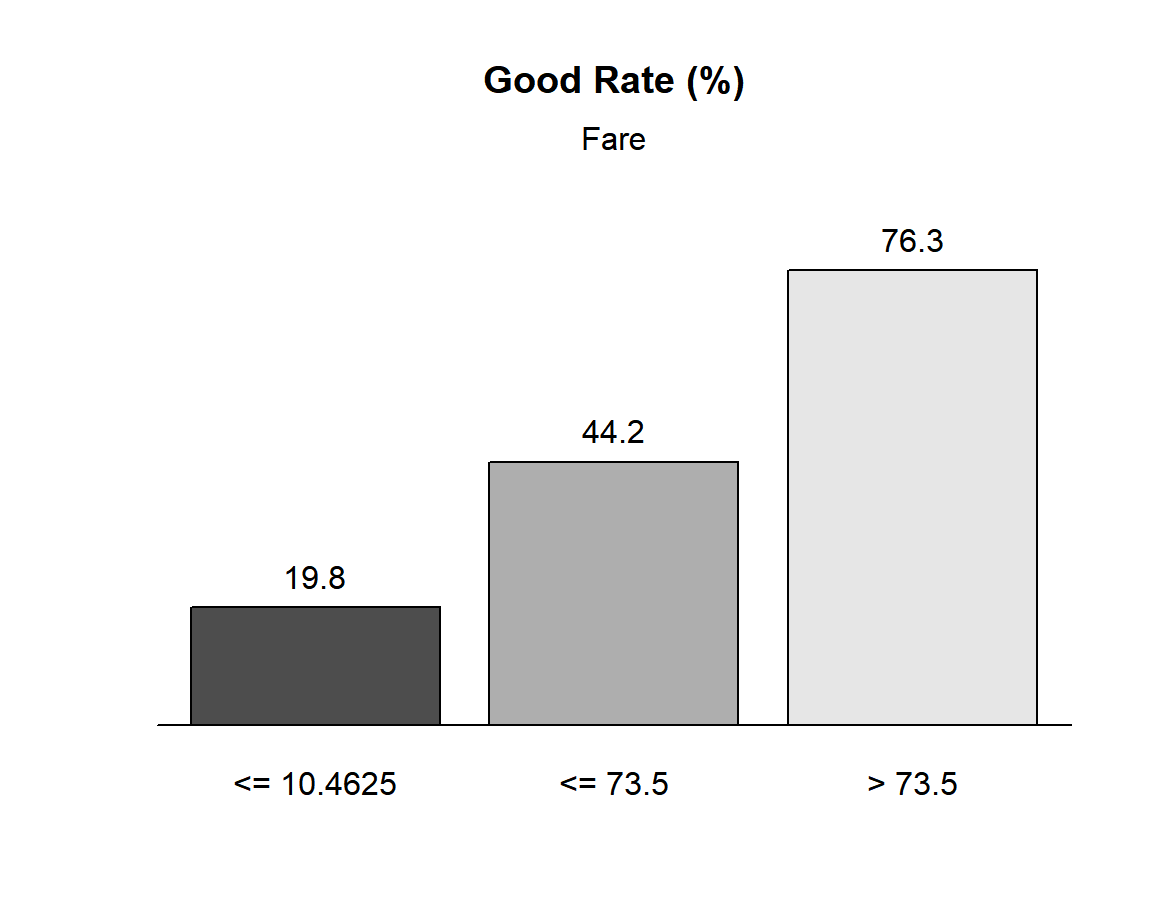
Frequence de la cible pour chaque modalite creee

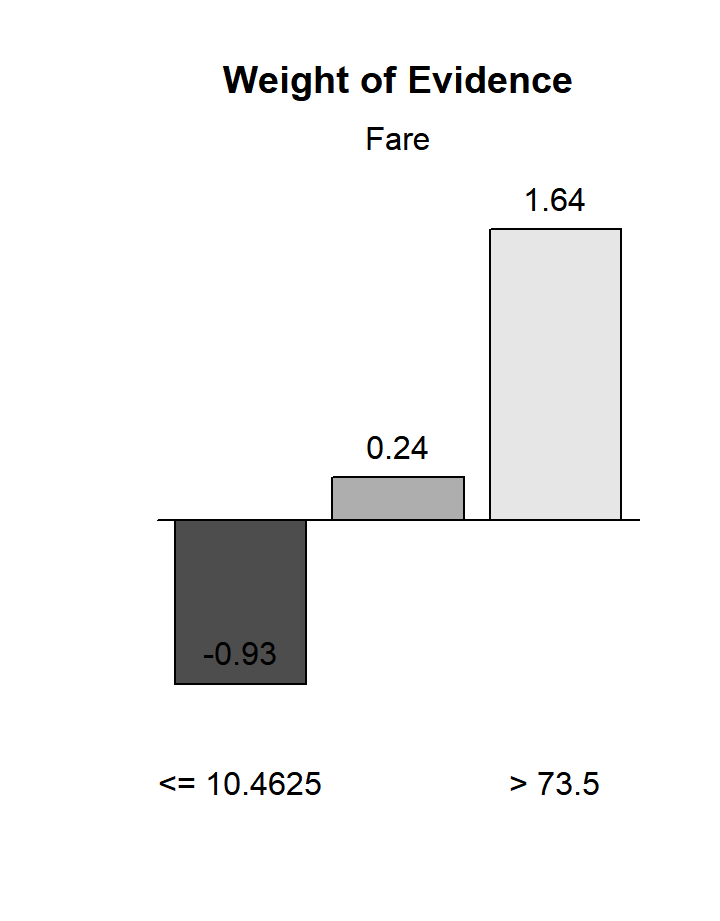
WoE de chaque modalite creee

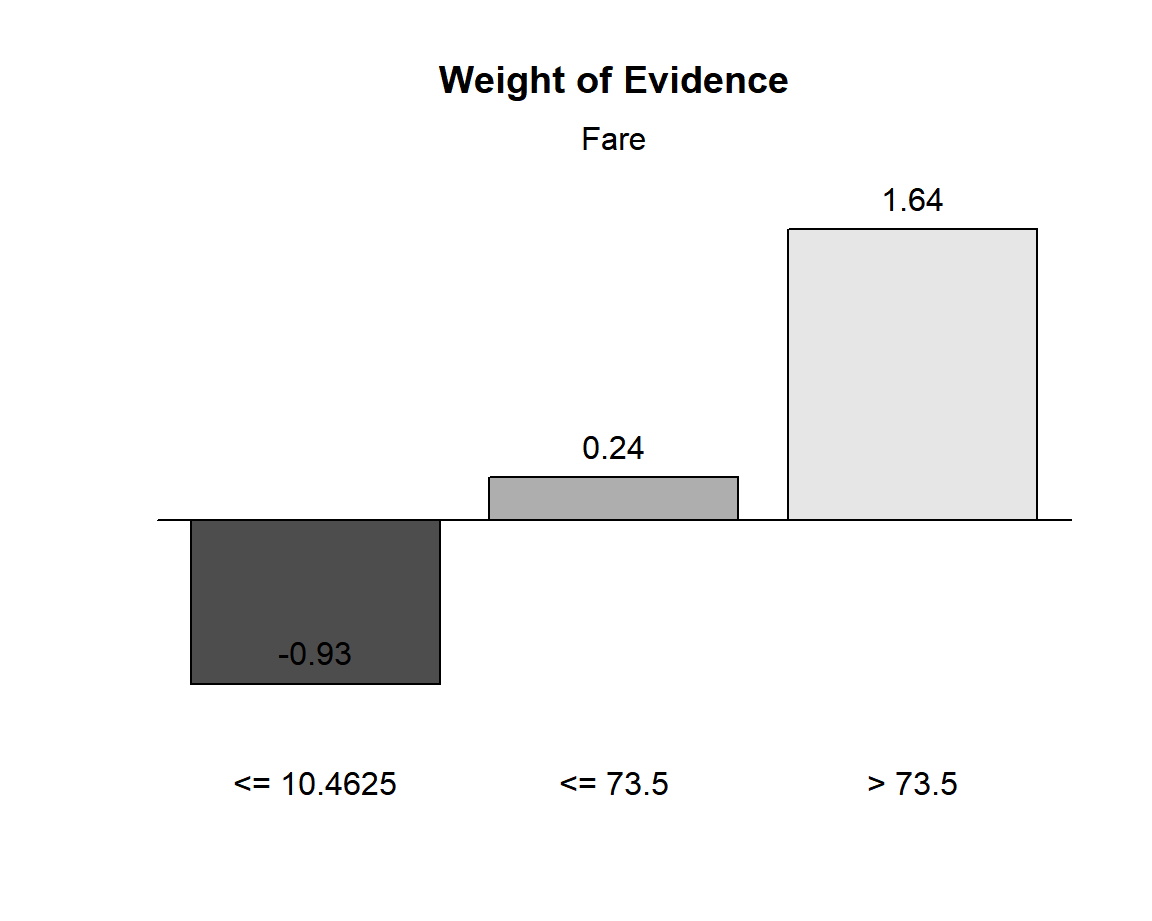
Note : WoE > 0 <=> Frequence cible > 38%

les indicateurs de qualite de la discretisation de la variable Fare

	Cutpoint	CntRec	CntGood	CntBad	CntCumRec	CntCumGood	CntCumBad	PctRec	GoodRate	BadRate	Odds	LnOdds	WoE	IV
1	<= 10.4625	339	67	272	339	67	272	0.3805	0.1976	0.8024	0.2463	-1.4011	-0.9278	0.2779
2	<= 73.5	455	201	254	794	268	526	0.5107	0.4418	0.5582	0.7913	-0.2340	0.2393	0.0299
3	> 73.5	97	74	23	891	342	549	0.1089	0.7629	0.2371	3.2174	1.1686	1.6419	0.2865
5	Total	891	342	549	NA	NA	NA	1.0000	0.3838	0.6162	0.6230	-0.4733	0.0000	0.5943

Un peu de theorie (et de formules mathematiques avec LaTeX) : Weight Of Evidence, Information Value

Le tableau d’indicateurs ci-dessus permet de se faire une idee de la qualite de la discretisation obtenue

• la colonne PctRec correspond au graphique des frequences des modalites, les colonnes GoodRate et WoE aux deux autres graphiques
• pour chaque modalite, l’indicateur WoE joue le meme role qu’un lift, mais il doit etre compare a 0 alors que le lift est compare a 1
• pour chaque variable qualitative, l’indicateur IV est positif, non majore et plus il est eleve, plus la variable est predictive de la cible.

Plus precisement, si on note \(Y\) la variable cible de valeurs 0 et 1 et \(X\) la variable explicative discretisee grace au package smbinning, de modalites a, b et c, alors on a les formules suivantes pour le Weight of Evidence et l’Information Value :

\[ WoE(i) = \log\left(\frac{P(X = i | Y = 1)} {P(X = i | Y = 0)}\right) = \log\left(\frac{\frac{P(Y = 1 | X = i)} {P(Y = 0 | X = i)}} {\frac{P(Y = 1)} {P(Y = 0)}}\right) \ et \ IV = \sum_{i = a,b,c} \left( P(X = i | Y = 1) - P(X = i | Y = 0) \right) \log\left(\frac{P(X = i | Y = 1)} {P(X = i | Y = 0)}\right)\] Le membre de droite de la 1ere formule est le logarithme de l’odds-ratio ( = le coefficient de la modalite \(i\) dans un modele de regression logistique). Si le WoE est positif cela indique que la modalite \(i\) favorise l’apparition de la cible, s’il est negatif c’est le contraire.

On prend en compte le % d’individus qui prennent cette modalite \((= P(X=i))\) en multipliant le WoE par la quantite \(P(X = i | Y = 1) - P(X = i | Y = 0)\), de cette facon on obtient un WoE pondere qui est toujours positif. Enfin on somme les WoE ponderes pour toutes les modalites de \(X\) ce qui donne l’Information Value totale.

Pour info l’IV est utilisee dans les regressions logistiques de credit scoring et on a les regles empiriques suivantes.

Information Value	Pouvoir de prediction
< 0,02	inutilisable
0,02 a 0,1	predicteur faible
0,1 a 0,3	predicteur moyen
0,3 a 0,5	predicteur fort
>0,5	suspect, trop beau pour etre vrai